Structure from Motion
5.1. Structure from Motion¶
Structure from Motion (SFM or SfM) is very similar to SLAM, except we are trying to estimate the pose of several cameras observing a set of unknown 3D landmarks.
%pip -q install gtbook # also installs latest gtsam pre-release
Note: you may need to restart the kernel to use updated packages.
import gtsam
import matplotlib.pyplot as plt
import numpy as np
from gtsam import symbol_shorthand
L = symbol_shorthand.L
X = symbol_shorthand.X
from gtsam.examples import SFMdata
from gtsam import (Cal3_S2, DoglegOptimizer,
GenericProjectionFactorCal3_S2, Marginals,
NonlinearFactorGraph, PinholeCameraCal3_S2, Point3,
Pose3, PriorFactorPoint3, PriorFactorPose3, Rot3, Values)
from gtsam.utils import plot
%matplotlib inline
Camera observations of landmarks (i.e. pixel coordinates) will be stored as Point2 (x, y).
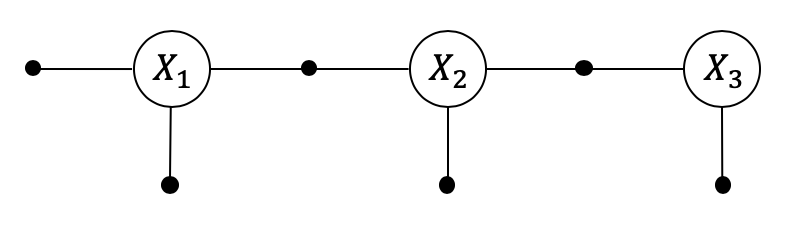
Each variable in the system (poses and landmarks) must be identified with a unique key. We can either use simple integer keys (1, 2, 3, …) or symbols (X1, X2, L1). Here we will use Symbols
In GTSAM, measurement functions are represented as ‘factors’. Several common factors have been provided with the library for solving robotics/SLAM/Bundle Adjustment problems. Here we will use Projection factors to model the camera’s landmark observations. Also, we will initialize the robot at some location using a Prior factor.
When the factors are created, we will add them to a Factor Graph. As the factors we are using are nonlinear factors, we will need a Nonlinear Factor Graph.
Finally, once all of the factors have been added to our factor graph, we will want to solve/optimize to graph to find the best (Maximum A Posteriori) set of variable values. GTSAM includes several nonlinear optimizers to perform this step. Here we will use a trust-region method known as Powell’s Degleg
The nonlinear solvers within GTSAM are iterative solvers, meaning they linearize the nonlinear functions around an initial linearization point, then solve the linear system to update the linearization point. This happens repeatedly until the solver converges to a consistent set of variable values. This requires us to specify an initial guess for each variable, held in a Values container.
# Define the camera calibration parameters
K = Cal3_S2(50.0, 50.0, 0.0, 50.0, 50.0)
# Define the camera observation noise model
measurement_noise = gtsam.noiseModel.Isotropic.Sigma(
2, 1.0) # one pixel in u and v
# Create the set of ground-truth landmarks
points = SFMdata.createPoints()
# Create the set of ground-truth poses
poses = SFMdata.createPoses(K)
# Create a factor graph
graph = NonlinearFactorGraph()
# Add a prior on pose x1. This indirectly specifies where the origin is.
# 0.3 rad std on roll,pitch,yaw and 0.1m on x,y,z
pose_noise = gtsam.noiseModel.Diagonal.Sigmas(
np.array([0.3, 0.3, 0.3, 0.1, 0.1, 0.1]))
factor = PriorFactorPose3(X(0), poses[0], pose_noise)
graph.push_back(factor)
# Simulated measurements from each camera pose, adding them to the factor graph
for i, pose in enumerate(poses):
camera = PinholeCameraCal3_S2(pose, K)
for j, point in enumerate(points):
measurement = camera.project(point)
factor = GenericProjectionFactorCal3_S2(
measurement, measurement_noise, X(i), L(j), K)
graph.push_back(factor)
Because the structure-from-motion problem has a scale ambiguity, the problem is still under-constrained Here we add a prior on the position of the first landmark. This fixes the scale by indicating the distance between the first camera and the first landmark. All other landmark positions are interpreted using this scale.
point_noise = gtsam.noiseModel.Isotropic.Sigma(3, 0.1)
factor = PriorFactorPoint3(L(0), points[0], point_noise)
graph.push_back(factor)
graph.print('Factor Graph:\n')
Factor Graph:
size: 66
Factor 0: PriorFactor on x0
prior mean: R: [
0, 0.242536, -0.970143;
1, -0, 0;
-0, -0.970143, -0.242536
]
t: 40 0 10
noise model: diagonal sigmas [0.3; 0.3; 0.3; 0.1; 0.1; 0.1];
Factor 1: GenericProjectionFactor, z = [
67.1796068;
37.5
]
keys = { x0 l0 }
noise model: unit (2)
Factor 2: GenericProjectionFactor, z = [
60.3077641;
37.5
]
keys = { x0 l1 }
noise model: unit (2)
Factor 3: GenericProjectionFactor, z = [
39.6922359;
37.5
]
keys = { x0 l2 }
noise model: unit (2)
Factor 4: GenericProjectionFactor, z = [
32.8203932;
37.5
]
keys = { x0 l3 }
noise model: unit (2)
Factor 5: GenericProjectionFactor, z = [
64.7253772;
67.8571429
]
keys = { x0 l4 }
noise model: unit (2)
Factor 6: GenericProjectionFactor, z = [
59.3706946;
56.8181818
]
keys = { x0 l5 }
noise model: unit (2)
Factor 7: GenericProjectionFactor, z = [
40.6293054;
56.8181818
]
keys = { x0 l6 }
noise model: unit (2)
Factor 8: GenericProjectionFactor, z = [
35.2746228;
67.8571429
]
keys = { x0 l7 }
noise model: unit (2)
Factor 9: GenericProjectionFactor, z = [
50;
37.5
]
keys = { x1 l0 }
noise model: unit (2)
Factor 10: GenericProjectionFactor, z = [
68.2217247;
37.5
]
keys = { x1 l1 }
noise model: unit (2)
Factor 11: GenericProjectionFactor, z = [
50;
37.5
]
keys = { x1 l2 }
noise model: unit (2)
Factor 12: GenericProjectionFactor, z = [
31.7782753;
37.5
]
keys = { x1 l3 }
noise model: unit (2)
Factor 13: GenericProjectionFactor, z = [
50;
71.9320653
]
keys = { x1 l4 }
noise model: unit (2)
Factor 14: GenericProjectionFactor, z = [
66.1970886;
61.1111111
]
keys = { x1 l5 }
noise model: unit (2)
Factor 15: GenericProjectionFactor, z = [
50;
55.465195
]
keys = { x1 l6 }
noise model: unit (2)
Factor 16: GenericProjectionFactor, z = [
33.8029114;
61.1111111
]
keys = { x1 l7 }
noise model: unit (2)
Factor 17: GenericProjectionFactor, z = [
32.8203932;
37.5
]
keys = { x2 l0 }
noise model: unit (2)
Factor 18: GenericProjectionFactor, z = [
67.1796068;
37.5
]
keys = { x2 l1 }
noise model: unit (2)
Factor 19: GenericProjectionFactor, z = [
60.3077641;
37.5
]
keys = { x2 l2 }
noise model: unit (2)
Factor 20: GenericProjectionFactor, z = [
39.6922359;
37.5
]
keys = { x2 l3 }
noise model: unit (2)
Factor 21: GenericProjectionFactor, z = [
35.2746228;
67.8571429
]
keys = { x2 l4 }
noise model: unit (2)
Factor 22: GenericProjectionFactor, z = [
64.7253772;
67.8571429
]
keys = { x2 l5 }
noise model: unit (2)
Factor 23: GenericProjectionFactor, z = [
59.3706946;
56.8181818
]
keys = { x2 l6 }
noise model: unit (2)
Factor 24: GenericProjectionFactor, z = [
40.6293054;
56.8181818
]
keys = { x2 l7 }
noise model: unit (2)
Factor 25: GenericProjectionFactor, z = [
31.7782753;
37.5
]
keys = { x3 l0 }
noise model: unit (2)
Factor 26: GenericProjectionFactor, z = [
50;
37.5
]
keys = { x3 l1 }
noise model: unit (2)
Factor 27: GenericProjectionFactor, z = [
68.2217247;
37.5
]
keys = { x3 l2 }
noise model: unit (2)
Factor 28: GenericProjectionFactor, z = [
50;
37.5
]
keys = { x3 l3 }
noise model: unit (2)
Factor 29: GenericProjectionFactor, z = [
33.8029114;
61.1111111
]
keys = { x3 l4 }
noise model: unit (2)
Factor 30: GenericProjectionFactor, z = [
50;
71.9320653
]
keys = { x3 l5 }
noise model: unit (2)
Factor 31: GenericProjectionFactor, z = [
66.1970886;
61.1111111
]
keys = { x3 l6 }
noise model: unit (2)
Factor 32: GenericProjectionFactor, z = [
50;
55.465195
]
keys = { x3 l7 }
noise model: unit (2)
Factor 33: GenericProjectionFactor, z = [
39.6922359;
37.5
]
keys = { x4 l0 }
noise model: unit (2)
Factor 34: GenericProjectionFactor, z = [
32.8203932;
37.5
]
keys = { x4 l1 }
noise model: unit (2)
Factor 35: GenericProjectionFactor, z = [
67.1796068;
37.5
]
keys = { x4 l2 }
noise model: unit (2)
Factor 36: GenericProjectionFactor, z = [
60.3077641;
37.5
]
keys = { x4 l3 }
noise model: unit (2)
Factor 37: GenericProjectionFactor, z = [
40.6293054;
56.8181818
]
keys = { x4 l4 }
noise model: unit (2)
Factor 38: GenericProjectionFactor, z = [
35.2746228;
67.8571429
]
keys = { x4 l5 }
noise model: unit (2)
Factor 39: GenericProjectionFactor, z = [
64.7253772;
67.8571429
]
keys = { x4 l6 }
noise model: unit (2)
Factor 40: GenericProjectionFactor, z = [
59.3706946;
56.8181818
]
keys = { x4 l7 }
noise model: unit (2)
Factor 41: GenericProjectionFactor, z = [
50;
37.5
]
keys = { x5 l0 }
noise model: unit (2)
Factor 42: GenericProjectionFactor, z = [
31.7782753;
37.5
]
keys = { x5 l1 }
noise model: unit (2)
Factor 43: GenericProjectionFactor, z = [
50;
37.5
]
keys = { x5 l2 }
noise model: unit (2)
Factor 44: GenericProjectionFactor, z = [
68.2217247;
37.5
]
keys = { x5 l3 }
noise model: unit (2)
Factor 45: GenericProjectionFactor, z = [
50;
55.465195
]
keys = { x5 l4 }
noise model: unit (2)
Factor 46: GenericProjectionFactor, z = [
33.8029114;
61.1111111
]
keys = { x5 l5 }
noise model: unit (2)
Factor 47: GenericProjectionFactor, z = [
50;
71.9320653
]
keys = { x5 l6 }
noise model: unit (2)
Factor 48: GenericProjectionFactor, z = [
66.1970886;
61.1111111
]
keys = { x5 l7 }
noise model: unit (2)
Factor 49: GenericProjectionFactor, z = [
60.3077641;
37.5
]
keys = { x6 l0 }
noise model: unit (2)
Factor 50: GenericProjectionFactor, z = [
39.6922359;
37.5
]
keys = { x6 l1 }
noise model: unit (2)
Factor 51: GenericProjectionFactor, z = [
32.8203932;
37.5
]
keys = { x6 l2 }
noise model: unit (2)
Factor 52: GenericProjectionFactor, z = [
67.1796068;
37.5
]
keys = { x6 l3 }
noise model: unit (2)
Factor 53: GenericProjectionFactor, z = [
59.3706946;
56.8181818
]
keys = { x6 l4 }
noise model: unit (2)
Factor 54: GenericProjectionFactor, z = [
40.6293054;
56.8181818
]
keys = { x6 l5 }
noise model: unit (2)
Factor 55: GenericProjectionFactor, z = [
35.2746228;
67.8571429
]
keys = { x6 l6 }
noise model: unit (2)
Factor 56: GenericProjectionFactor, z = [
64.7253772;
67.8571429
]
keys = { x6 l7 }
noise model: unit (2)
Factor 57: GenericProjectionFactor, z = [
68.2217247;
37.5
]
keys = { x7 l0 }
noise model: unit (2)
Factor 58: GenericProjectionFactor, z = [
50;
37.5
]
keys = { x7 l1 }
noise model: unit (2)
Factor 59: GenericProjectionFactor, z = [
31.7782753;
37.5
]
keys = { x7 l2 }
noise model: unit (2)
Factor 60: GenericProjectionFactor, z = [
50;
37.5
]
keys = { x7 l3 }
noise model: unit (2)
Factor 61: GenericProjectionFactor, z = [
66.1970886;
61.1111111
]
keys = { x7 l4 }
noise model: unit (2)
Factor 62: GenericProjectionFactor, z = [
50;
55.465195
]
keys = { x7 l5 }
noise model: unit (2)
Factor 63: GenericProjectionFactor, z = [
33.8029114;
61.1111111
]
keys = { x7 l6 }
noise model: unit (2)
Factor 64: GenericProjectionFactor, z = [
50;
71.9320653
]
keys = { x7 l7 }
noise model: unit (2)
Factor 65: PriorFactor on l0
prior mean: [
10;
10;
10
]
isotropic dim=3 sigma=0.1
Create the data structure to hold the initial estimate to the solution Intentionally initialize the variables off from the ground truth
initial_estimate = Values()
for i, pose in enumerate(poses):
transformed_pose = pose.retract(0.1*np.random.randn(6, 1))
initial_estimate.insert(X(i), transformed_pose)
for j, point in enumerate(points):
transformed_point = point + 0.1*np.random.randn(3)
initial_estimate.insert(L(j), transformed_point)
initial_estimate.print('Initial Estimates:\n')
Initial Estimates:
Values with 16 values:
Value l0: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
10.1610152;
10.1745789;
10.0150178
]
Value l1: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
-10.1102248;
9.99350882;
9.90414938
]
Value l2: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
-9.93187048;
-10.0854579;
10.1119008
]
Value l3: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
9.86423774;
-9.89195433;
10.1032942
]
Value l4: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
9.93460759;
9.92311056;
-10.1511104
]
Value l5: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
-9.81261829;
9.9817152;
-9.87510434
]
Value l6: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
-9.95108764;
-9.99542684;
-10.0617022
]
Value l7: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
9.95946916;
-10.0990484;
-9.87889377
]
Value x0: (gtsam::Pose3)
R: [
0.239205784, 0.22802534, -0.94381409;
0.970967045, -0.0542788531, 0.232973826;
0.00189478947, -0.972141065, -0.234388906
]
t: 40.0938109 -0.0467862268 9.79643798
Value x1: (gtsam::Pose3)
R: [
-0.486264, 0.195253703, -0.85171786;
0.864907311, 0.246346484, -0.437319966;
0.124429358, -0.949309961, -0.288665782
]
t: 28.2069251 28.2007517 9.86712045
Value x2: (gtsam::Pose3)
R: [
-0.966907054, 0.249970559, -0.0510437886;
0.0980901008, 0.179540739, -0.978848025;
-0.235518748, -0.95146195, -0.198118844
]
t: 0.0389124968 39.9329867 9.95978664
Value x3: (gtsam::Pose3)
R: [
-0.624238932, -0.357160725, 0.694810746;
-0.73943375, -0.0169005758, -0.673017162;
0.252117999, -0.933890029, -0.253546697
]
t: -28.2363316 28.2904554 10.0204455
Value x4: (gtsam::Pose3)
R: [
0.0710064082, -0.23248816, 0.970003786;
-0.990821544, 0.0957005988, 0.0954676017;
-0.11502503, -0.967879461, -0.223558922
]
t: -40.2211595 -0.134540484 10.1045333
Value x5: (gtsam::Pose3)
R: [
0.756936176, -0.108120331, 0.644482443;
-0.653421702, -0.111089594, 0.748798492;
-0.00936504746, -0.987911482, -0.154735903
]
t: -28.2877174 -28.1586639 9.91260829
Value x6: (gtsam::Pose3)
R: [
0.990085348, 0.117909753, -0.0763432635;
0.107699883, -0.288308688, 0.951461421;
0.0901761553, -0.950250173, -0.298149074
]
t: 0.155274926 -40.1116881 10.0404074
Value x7: (gtsam::Pose3)
R: [
0.790270222, 0.20373813, -0.577895968;
0.604798864, -0.107829103, 0.789044497;
0.0984444466, -0.973069195, -0.208434719
]
t: 28.1571957 -28.2358214 10.0155201
Optimize the graph and print results
params = gtsam.DoglegParams()
params.setVerbosity('TERMINATION')
optimizer = DoglegOptimizer(graph, initial_estimate, params)
print('Optimizing:')
result = optimizer.optimize()
result.print('Final results:\n')
print('initial error = {}'.format(graph.error(initial_estimate)))
print('final error = {}'.format(graph.error(result)))
Optimizing:
Final results:
Values with 16 values:
Value l0: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
10;
10;
10
]
converged
errorThreshold: 1.71912811e-23 <? 0
absoluteDecrease: 1.73334473178e-10 <? 1e-05
relativeDecrease: 1 <? 1e-05
iterations: 5 >? 100
Value l1: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
-10;
10;
10
]
Value l2: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
-10;
-10;
10
]
Value l3: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
10;
-10;
10
]
Value l4: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
10;
10;
-10
]
Value l5: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
-10;
10;
-10
]
Value l6: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
-10;
-10;
-10
]
Value l7: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
10;
-10;
-10
]
Value x0: (gtsam::Pose3)
R: [
-5.81838611259e-17, 0.242535625036, -0.970142500145;
1, 1.68892561347e-16, -5.38733123185e-17;
1.47363545273e-16, -0.970142500145, -0.242535625036
]
t: 40 -2.5060460778e-19 10
Value x1: (gtsam::Pose3)
R: [
-0.707106781187, 0.171498585143, -0.68599434057;
0.707106781187, 0.171498585143, -0.68599434057;
5.18649860129e-16, -0.970142500145, -0.242535625036
]
t: 28.2842712475 28.2842712475 10
Value x2: (gtsam::Pose3)
R: [
-1, -3.29030031039e-15, 8.71302416831e-15;
-9.25482712212e-15, 0.242535625036, -0.970142500145;
1.11941448023e-15, -0.970142500145, -0.242535625036
]
t: -4.02504442824e-13 40 10
Value x3: (gtsam::Pose3)
R: [
-0.707106781187, -0.171498585142, 0.68599434057;
-0.707106781187, 0.171498585142, -0.68599434057;
-1.546160487e-15, -0.970142500145, -0.242535625036
]
t: -28.2842712475 28.2842712475 10
Value x4: (gtsam::Pose3)
R: [
2.01561029756e-15, -0.242535625036, 0.970142500145;
-1, -1.44313354536e-15, 1.72151196395e-15;
1.00827518217e-15, -0.970142500145, -0.242535625036
]
t: -40 -1.11991947532e-14 10
Value x5: (gtsam::Pose3)
R: [
0.707106781187, -0.171498585143, 0.68599434057;
-0.707106781187, -0.171498585143, 0.68599434057;
-6.90453081923e-16, -0.970142500145, -0.242535625036
]
t: -28.2842712475 -28.2842712475 10
Value x6: (gtsam::Pose3)
R: [
1, 9.63889411922e-16, -1.00159223829e-14;
9.94817190341e-15, -0.242535625036, 0.970142500145;
-1.55265228461e-15, -0.970142500145, -0.242535625036
]
t: 5.11947451298e-13 -40 10
Value x7: (gtsam::Pose3)
R: [
0.707106781187, 0.171498585143, -0.68599434057;
0.707106781187, -0.171498585143, 0.68599434057;
-6.19236781409e-16, -0.970142500145, -0.242535625036
]
t: 28.2842712475 -28.2842712475 10
initial error = 2717.215012510053
final error = 1.7191281142028447e-23
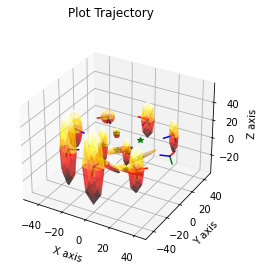
marginals = Marginals(graph, result)
plot.plot_3d_points(1, result, marginals=marginals)
plot.plot_trajectory(1, result, marginals=marginals, scale=8)
plot.set_axes_equal(1)
plt.show()