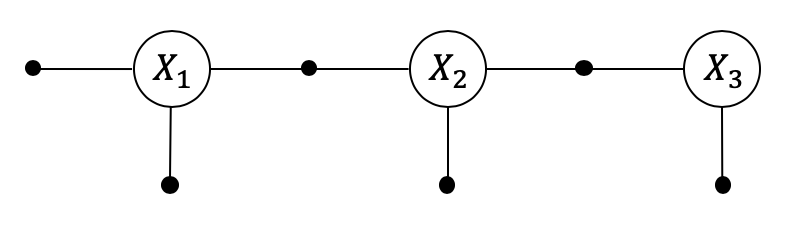
Planar SLAM
2.4. Planar SLAM¶
“True” Simultaneous Localization and Mapping optimizes for both the unknown robot trajectory and unknown landmarks. The simple example below sketches out how this would work with GTSAM, in the 2D (Pose2) case.
%pip -q install gtbook # also installs latest gtsam pre-release
Note: you may need to restart the kernel to use updated packages.
import gtsam
import numpy as np
from gtsam.symbol_shorthand import L, X
# Create noise models
PRIOR_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.3, 0.3, 0.1]))
ODOMETRY_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.2, 0.2, 0.1]))
MEASUREMENT_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.1, 0.2]))
# Create an empty nonlinear factor graph
graph = gtsam.NonlinearFactorGraph()
# Add a prior on pose X1 at the origin. A prior factor consists of a mean and a noise model
graph.add(
gtsam.PriorFactorPose2(X(1), gtsam.Pose2(0.0, 0.0, 0.0), PRIOR_NOISE))
# Add odometry factors between X1,X2 and X2,X3, respectively
graph.add(
gtsam.BetweenFactorPose2(X(1), X(2), gtsam.Pose2(2.0, 0.0, 0.0),
ODOMETRY_NOISE))
graph.add(
gtsam.BetweenFactorPose2(X(2), X(3), gtsam.Pose2(2.0, 0.0, 0.0),
ODOMETRY_NOISE))
# Add Range-Bearing measurements to two different landmarks L1 and L2
graph.add(
gtsam.BearingRangeFactor2D(X(1), L(1), gtsam.Rot2.fromDegrees(45),
np.sqrt(4.0 + 4.0), MEASUREMENT_NOISE))
graph.add(
gtsam.BearingRangeFactor2D(X(2), L(1), gtsam.Rot2.fromDegrees(90), 2.0,
MEASUREMENT_NOISE))
graph.add(
gtsam.BearingRangeFactor2D(X(3), L(2), gtsam.Rot2.fromDegrees(90), 2.0,
MEASUREMENT_NOISE))
# Print graph
print("Factor Graph:\n{}".format(graph))
Factor Graph:
NonlinearFactorGraph: size: 6
Factor 0: PriorFactor on x1
prior mean: (0, 0, 0)
noise model: diagonal sigmas [0.3; 0.3; 0.1];
Factor 1: BetweenFactor(x1,x2)
measured: (2, 0, 0)
noise model: diagonal sigmas [0.2; 0.2; 0.1];
Factor 2: BetweenFactor(x2,x3)
measured: (2, 0, 0)
noise model: diagonal sigmas [0.2; 0.2; 0.1];
Factor 3: BearingRangeFactor
Factor 3: keys = { x1 l1 }
noise model: diagonal sigmas [0.1; 0.2];
ExpressionFactor with measurement: bearing : 0.785398163
range 2.82842712
Factor 4: BearingRangeFactor
Factor 4: keys = { x2 l1 }
noise model: diagonal sigmas [0.1; 0.2];
ExpressionFactor with measurement: bearing : 1.57079633
range 2
Factor 5: BearingRangeFactor
Factor 5: keys = { x3 l2 }
noise model: diagonal sigmas [0.1; 0.2];
ExpressionFactor with measurement: bearing : 1.57079633
range 2
# Create (deliberately inaccurate) initial estimate
initial_estimate = gtsam.Values()
initial_estimate.insert(X(1), gtsam.Pose2(-0.25, 0.20, 0.15))
initial_estimate.insert(X(2), gtsam.Pose2(2.30, 0.10, -0.20))
initial_estimate.insert(X(3), gtsam.Pose2(4.10, 0.10, 0.10))
initial_estimate.insert(L(1), gtsam.Point2(1.80, 2.10))
initial_estimate.insert(L(2), gtsam.Point2(4.10, 1.80))
# Print
print("Initial Estimate:\n{}".format(initial_estimate))
Initial Estimate:
Values with 5 values:
Value l1: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
1.8;
2.1
]
Value l2: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
4.1;
1.8
]
Value x1: (gtsam::Pose2)
(-0.25, 0.2, 0.15)
Value x2: (gtsam::Pose2)
(2.3, 0.1, -0.2)
Value x3: (gtsam::Pose2)
(4.1, 0.1, 0.1)
Optimize using Levenberg-Marquardt optimization.
The optimizer accepts an optional set of configuration parameters, controlling things like convergence criteria, the type of linear system solver to use, and the amount of information displayed during optimization. Here we will use the default set of parameters. See the documentation for the full set of parameters.
params = gtsam.LevenbergMarquardtParams()
optimizer = gtsam.LevenbergMarquardtOptimizer(graph, initial_estimate,
params)
result = optimizer.optimize()
print("\nFinal Result:\n{}".format(result))
Final Result:
Values with 5 values:
Value l1: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
2;
2
]
Value l2: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
4;
2
]
Value x1: (gtsam::Pose2)
(-5.72151287e-16, -2.62210479e-16, -8.93526824e-17)
Value x2: (gtsam::Pose2)
(2, -5.828131e-15, -6.88657241e-16)
Value x3: (gtsam::Pose2)
(4, -1.06845396e-14, -6.47850202e-16)
Calculate and print marginal covariances for all variables
marginals = gtsam.Marginals(graph, result)
for (key, s) in [(X(1), "X1"), (X(2), "X2"), (X(3), "X3"), (L(1), "L1"),
(L(2), "L2")]:
print("{} covariance:\n{}\n".format(s,
marginals.marginalCovariance(key)))
X1 covariance:
[[ 9.00000000e-02 -2.15827356e-17 -1.27897692e-17]
[-2.15827356e-17 9.00000000e-02 3.06709120e-33]
[-1.27897692e-17 3.06709120e-33 1.00000000e-02]]
X2 covariance:
[[ 0.12096774 -0.00129032 0.00451613]
[-0.00129032 0.1583871 0.02064516]
[ 0.00451613 0.02064516 0.01774194]]
X3 covariance:
[[0.16096774 0.00774194 0.00451613]
[0.00774194 0.35193548 0.05612903]
[0.00451613 0.05612903 0.02774194]]
L1 covariance:
[[ 0.16870968 -0.04774194]
[-0.04774194 0.16354839]]
L2 covariance:
[[ 0.29387097 -0.10451613]
[-0.10451613 0.39193548]]